最大子数组问题及其历史
20世纪70年代末,瑞典数学家ulf greNANDer一直在讨论一个问题:如何比暴力破解更有效地分析二维图像数据数组?那时的计算机速度很慢,图片相对于 ram 来说也很大。更糟糕的是,在最坏的情况下,暴力破解需要 o(n^6) 时间(六次时间复杂度)。
首先,grenandier 简化了问题:给定一个一维数字数组,如何最有效地找到总和最大的连续子数组?
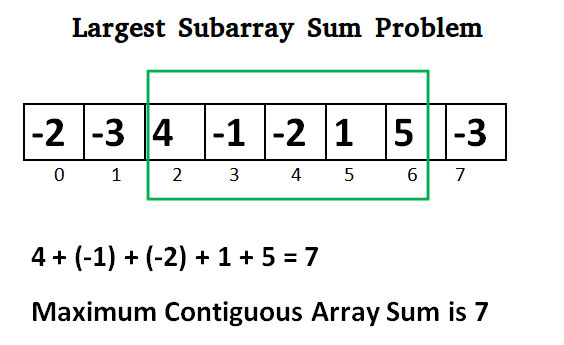
蛮力:一种具有立方时间复杂度的简单方法
蛮力,分析一维数组的时间是分析二维数组的一半,所以 o(n^3) 来检查每个可能的组合(立方时间复杂度)。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
def max_subarray_brute_force(arr):
max_sum = arr[0] # assumes arr has a length
# iterate over all possible subarrays
for i in range(len(arr)):
for j in range(i, len(arr)):
current_sum = 0
# sum the elements of the subarray arr[i:j+1]
for k in range(i, j + 1):
current_sum += arr[k]
# update max_sum if the current sum is greater
max_sum = max(max_sum, current_sum)
return max_sum
print(max_subarray_brute_force([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")
|
grenander 的 o(n²) 优化:向前迈出了一步
grenander 将其改进为 o(n^2) 解决方案。我在研究中找不到他的代码,但我的猜测是他只是摆脱了最内层的循环,该循环将两个索引之间的所有数字相加。相反,我们可以在迭代子数组时保留运行总和,从而将循环次数从三个减少到两个。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
def max_subarray_optimized(arr):
max_sum = arr[0] # assumes arr has a length
# iterate over all possible starting points of the subarray
for i in range(len(arr)):
current_sum = 0
# sum the elements of the subarray starting from arr[i]
for j in range(i, len(arr)):
current_sum += arr[j]
# update max_sum if the current sum is greater
max_sum = max(max_sum, current_sum)
return max_sum
|
shamos 的分而治之:将问题分解为 o(n log n)
grenander 向计算机科学家 michael shamos 展示了这个问题。 shamos思考了一晚上,想出了一个分而治之的方法,o(n log n)。
真是太聪明了。想法是将数组分成两半,然后递归地找到每一半的最大子数组和以及穿过中点的子数组。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
def max_crossing_sum(arr, left, mid, right):
# left of mid
left_sum = float('-inf')
current_sum = 0
for i in range(mid, left - 1, -1):
current_sum += arr[i]
left_sum = max(left_sum, current_sum)
# right of mid
right_sum = float('inf')
current_sum = 0
for i in range(mid + 1, right + 1):
current_sum += arr[i]
right_sum = max(right_sum, current_sum)
# sum of elements on the left and right of mid, which is the maximum sum that crosses the midpoint
return left_sum + right_sum
def max_subarray_divide_and_conquer(arr, left, right):
# base case: only one element
if left == right:
return arr[left]
# find the midpoint
mid = (left + right)
# recursively find the maximum subarray sum for the left and right halves
left_sum = max_subarray_divide_and_conquer(arr, left, mid)
right_sum = max_subarray_divide_and_conquer(arr, mid + 1, right)
cross_sum = max_crossing_sum(arr, left, mid, right)
# return the maximum of the three possible cases
return max(left_sum, right_sum, cross_sum)
def max_subarray(arr):
return max_subarray_divide_and_conquer(arr, 0, len(arr) - 1)
print(max_subarray([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")
|
这将时间复杂度降低到 o(nlogn) 时间,因为首先将数组分为两半 (o(logn)),然后找到最大交叉子数组需要 o(n)
kadane 算法:优雅的 o(n) 解决方案
统计学家 jay kadane 看了代码,立即发现 shamos 的解决方案未能使用邻接约束作为解决方案的一部分。
这是他意识到的
-如果数组只有负数,那么答案将始终是数组中最大的数字,假设我们不允许空子数组。
-如果数组只有正数,答案总是将整个数组相加。
-如果你有一个同时包含正数和负数的数组,那么你可以一步步遍历该数组。如果在任何时候您正在查看的数字大于其之前的所有数字的总和,则解决方案不能包含任何先前的数字。因此,您从当前数字开始一个新的总和,同时跟踪迄今为止遇到的最大总和。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
maxSubArray(nums):
# avoiding type errors or index out of bounds errors
if nums is None or len(nums) == 0:
return 0
max_sum = nums[0] # max sum can't be smaller than any given element
curr_sum = 0
# Kadane's algorithm
for num in nums:
curr_sum = max(num, curr_sum + num)
max_sum = max(curr_sum, max_sum)
return max_sum
|
我喜欢这个算法的原因是它可以应用于许多其他问题。尝试调整它来解决这些 leetcode 问题:
一和零
圆形子数组的最大和
最小子数组总和
最大升序子数组和
最大产品子数组
连续子数组和
最大交替和子数组(高级)
矩形的最大和不大于 k