最大点数与成本

也想出现在这里？点击联系我~

1937 年。最大积分数量与成本

难度：中等

主题： 数组、动态规划

给你一个 m x n 整数矩阵点（0 索引）。从 0 点开始，您希望最大化可以从矩阵中获得的点数。

要获得积分，您必须在每一行中选择一个单元格。选择坐标 (r, c) 处的单元格将为您的分数添加 分 [r][c]。

但是，如果您选择的单元格距离您在上一行中选择的单元格太远，您将失去分数。对于每两个相邻行 r 和 r + 1（其中 0 1_{) 和 (r + 1, c}2_{) 处选取单元格将}减去 abs (c1 _{– c}2_{) 来自您的分数。}返回

您能获得的最大积分。

abs(x) 定义为：

x 为 x >= 0.

-x 代表 x

示例1：

• 输入： l1 = [2,4,3], l2 = [5,6,4]
• 输出： 9
• 说明：
  蓝色单元格表示要选取的最佳单元格，其坐标为 (0, 2)、(1, 1) 和 (2, 0)。

  您将 3 + 5 + 3 = 11 加到您的分数上。

  但是，你必须从你的分数中减去abs(2 – 1) + abs(1 – 0) = 2。

  您的最终得分是 11 – 2 = 9.

示例2：

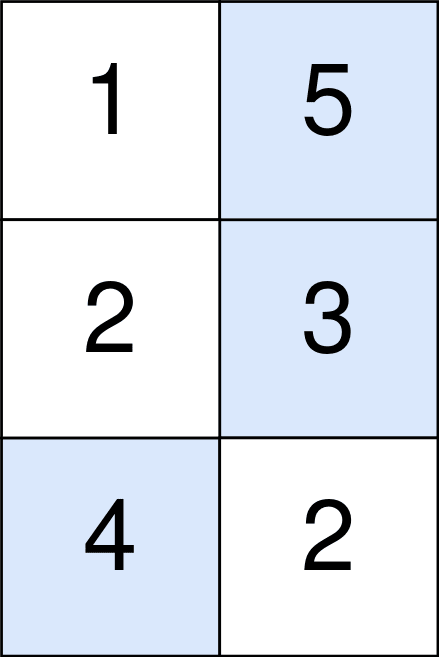
• 输入： 点 = [[1,5],[2,3],[4,2]]
• 输出： 11
• 说明：
  蓝色单元格表示要选取的最佳单元格，其坐标为 (0, 1)、(1, 1) 和 (2, 0)。

  您将 5 + 3 + 4 = 12 加到您的分数上。

  但是，你必须从你的分数中减去abs(1 – 1) + abs(1 – 0) = 1。

  您的最终得分是 12 – 1 = 11。

限制：

m == 点.长度

n == 点[r].长度

1 51 50 5

提示：

尝试使用动态规划。

dp[i][j] 是如果点[i][j] 是您最近选择的单元格时您可以拥有的最大点数。

解决方案：

我们可以将解决方案分解为几个步骤：

第 1 步：定义 dp 数组

我们将使用 2d 数组 dp，其中 dp[i][j] 表示通过选择第 i 行和 j 列的单元格可以获得的最大点数。

步骤2：初始化dp阵列

初始化第一行 dp 与第一行点相同，因为没有前面的行可以减去成本。

步骤 3：计算每行的 dp 值

对于每个后续行，我们考虑到从前一行切换的成本来计算每列的最大可能点。

为了高效计算从第 i-1 行到第 i 行的转换，我们可以使用左右两个辅助数组：

left[j] 将存储我们可以为第 j 列实现的最大值，仅考虑从左侧的转换。

right[j] 将存储我们可以为第 j 列实现的最大值，仅考虑从右侧的转换。

步骤 4：更新每行的 dp

对于第 i 行中的每一列 j：

使用 left[j] 或 right[j] 中的最大值加上点 [i][j] 来更新 dp[i][j]。

步骤 5：返回最后一行的最大值

结果将是 dp 数组最后一行的最大值。

让我们用 php 实现这个解决方案：

1937。最大积分与费用

解释：

• 左数组和右数组： 这些帮助我们通过考虑前一行的值来计算每个单元格可以获得的最大分数，有效地考虑跨列移动的惩罚。
• 动态编程方法： 此方法确保每一行都是基于前一行计算的，使得解决方案可针对大型矩阵进行扩展。

这种方法的时间复杂度为 (o(m times n))，在给定约束的情况下是有效的。

联系链接

如果您发现本系列有帮助，请考虑在 Github 上给

存储库 一颗星，或在您最喜欢的社交网络上分享该帖子?。您的支持对我来说意义重大！

如果您想要更多类似的有用内容，请随时关注我：

• 领英
• github