1905 年。计算子岛屿
难度:中等
给定两个 m x n 二进制矩阵 grid1 和 grid2,其中仅包含 0(代表水)和 1(代表土地)。 岛屿是一组由1连接的4向(水平或垂直)。网格之外的任何细胞都被视为水细胞。
如果 grid1 中的一个岛包含所有构成 grid2 中这个岛的单元格,则 grid2 中的岛被视为子岛 .
返回grid2中被视为子岛的数量个岛屿。
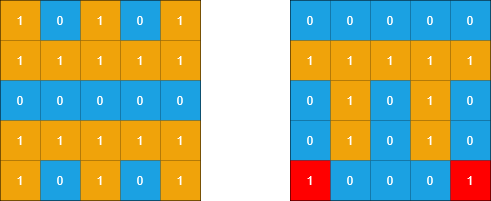
示例1:
- 输入: grid1 = [[1,1,1,0,0],[0,1,1,1,1],[0,0,0,0,0],[1, 0,0,0,0],[1,1,0,1,1]], grid2 = [[1,1,1,0,0],[0,0,1,1,1],[ 0,1,0,0,0],[1,0,1,1,0],[0,1,0,1,0]]
- 输出: 3
- 说明:
- 上图中,左边的网格是grid1,右边的网格是grid2。
- grid2 中红色的 1 被认为是子岛的一部分。共有三个子岛。
示例2:
- 输入: grid1 = [[1,0,1,0,1],[1,1,1,1,1],[0,0,0,0,0],[1, 1,1,1,1],[1,0,1,0,1]], grid2 = [[0,0,0,0,0],[1,1,1,1,1],[ 0,1,0,1,0],[0,1,0,1,0],[1,0,0,0,1]]
- 输出: 2
- 说明:
- 上图中,左边的网格是grid1,右边的网格是grid2。
- grid2 中红色的 1 被认为是子岛的一部分。有两个子岛。
约束:
- m == grid1.length == grid2.length
- n == grid1[i].length == grid2[i].length
- 1
- grid1[i][j] 和 grid2[i][j] 为 0 或 1。
提示:
- 让我们使用洪水填充来迭代第二个网格的岛屿
- 让我们注意,如果第二个网格中的一个岛上的所有单元格都由第一个网格中的土地表示,那么它们就会连接起来,从而使该岛成为一个子岛
解决方案:
我们将使用深度优先搜索 (dfs) 方法来探索 grid2 中的岛屿,并检查每个岛屿是否完全包含在 grid1 中的相应岛屿内。以下是我们实施该解决方案的方法:
步骤:
- 遍历网格:我们将迭代 grid2 中的每个单元格。
- 识别 grid2 中的岛屿:当我们在 grid2 中遇到陆地单元 (1) 时,我们将使用 dfs 探索整个岛屿。
- 检查子岛情况: 在 grid2 中的一个岛屿上执行 dfs 时,我们将检查 grid1 中所有对应的单元格是否也是陆地单元格。如果是的话,该岛就是一个子岛。
- 计算子岛数: 对于 grid2 中满足子岛条件的每个岛屿,我们将增加子岛数。
让我们用 php 实现这个解决方案:1905。数一下子岛屿
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 |
|
解释:
- dfs 函数: dfs 函数探索 grid2 中的岛屿,并检查 grid1 中相应的单元格是否都是陆地单元格。如果 grid2 中的任何单元格是陆地,但 grid1 中相应的单元格是水,则 grid2 中的岛屿不是子岛。
- 标记已访问: 当我们遍历 grid2 时,我们通过将单元格设置为 0 将其标记为已访问。
- 主循环:我们迭代grid2中的所有单元格。每当我们发现一个尚未访问过的陆地单元时,我们都会启动 dfs 来检查它是否是子岛的一部分。
时间复杂度:
时间复杂度为 (o(m × n)),其中 m 是行数,n 是列数。这是因为我们可能会访问每个单元格一次。
该解决方案应该在给定的限制内有效地工作。